IT技術者のAIに関する雑記

AI関連のMicrosoft技術やデータサイエンスの話をメインに。

Bot Serviceの.NET SDKであるDialogからQnAMakerを呼びたい場合

Bot Serviceの.NET SDKを使ってQnAMakerを呼び出す基本的な方法は、GitHubにあるサンプルのように、MessageControllerからQnAMakerDialogを継承したクラス、例えばQnADialogを以下のように呼び出すやり方になります。

public async Task<HttpResponseMessage> Post([FromBody]Activity activity)
        {
            if (activity.Type == ActivityTypes.Message)
            {
                await Conversation.SendAsync(activity, () => new Dialogs.QnADialog());
            }
......


サンプルはこちら：
BotBuilder-CognitiveServices/CSharp/Samples at master · Microsoft/BotBuilder-CognitiveServices · GitHub


ですが、いきなりFAQに行くのではなく、Botでの会話フローの中でQnAMakerを呼び出したいですよね。つまり、MessageControllerからRootDialogを呼び出し、その中でQnAMakerを呼び出したいということになります。

通常、ダイアログから別のダイアログを呼び出す場合は、マニュアルに記述されているようにIDialogContext .Forwardを使って別のダイアログの呼び出しを行います。
Manage conversation flow with dialogs - Bot Service | Microsoft Docs


IDialogContext .Forwardは別ダイアログのStartAsyncメソッドを呼び出すのですが、QnAMakerDialogに対してはうまく動かず(StartAsyncを使っていない？)、ダイアログ呼び出し後の処理に移ってしまうようです。

QnAMakerのREST APIを直接呼び出すことで対応できるのですが、.NET SDKを使った場合の対応方法については継続して調査しようと思っています。

Azure Machine Learning WorkbenchからSparkクラスタを使う場合の注意点

最近リリースされたAzure Machine Learning Workbenchは、機械学習の実行環境を

  • ローカルPC
  • ローカルPC上のDocker

から選択できます。

リモートPCのDocker及びAzure HDInsightのSparkクラスタを使う際の設定方法については

Azure ML のコンピューティング ターゲットとして DSVM と HDI を作成する方法 | Microsoft Docs

に記述されているのですが、追加の設定が必要になる場合があります。

上記のドキュメントに記載されている設定手順は

  1. Sparkクラスタを作成(OSはLinux、バージョンはSpark2.1 (HDI 3.6)を選択)
  2. Sparkクラスタをコンピューティングターゲットとしてアタッチ

になります。例えばクラスタ名がmksparkcluster01の場合には、Azure Machine Learning Workbenchからコマンドプロンプトを開き(FileメニューからOpen Command Promptメニューを選択)、以下のコマンドを実行すると、Sparkクラスタにアタッチできます。

az ml computetarget attach --name mksparkcluster01 --address mksparkcluster01.azurehdinsight.net --username <ssh username> --password <ssh password> --type cluster
az ml experiment prepare -c mksparkcluster01


ただし、これで機械学習のスクリプトを記述して実行すると、以下のエラーが発生することがあります。

ImportError: libmpi_cxx.so.1: cannot open shared object file: No such file or directory


この問題は、MMLSpark (Microsoft Machine Learning Library for Apache Spark) を明示的にSparkクラスタにインストールすることで解消されます (プロジェクトフォルダ配下のaml_config/spark_dependencies.ymlに記述された構成に従ってMMLSparkはインストールされるはずなのですが。。)。


MMLSparkのインストール方法は以下になります。

Azureポータルで作成したHDInsightクラスタを選択し、「スクリプト操作」メニューを選択
f:id:masakykato:20171108132744p:plain

「新規で送信」ボタンをクリックし、スクリプト操作として以下を入力します。

  • 名前：(適切な名前を入力、例えばMMLSparkInstall)
  • ノードの種類：「ヘッド」と「ワーカー」を選択

f:id:masakykato:20171108133237p:plain

「作成」ボタンをクリックすると、ヘッドノードとワーカーノードに、MMLSparkがインストールされます。


最新のスクリプトは以下のGitHubで確認してください。
github.com

Cognitive Toolkitを使ってみる ~ 深層学習を数値データの二値分類から初めてみよう

深層学習の入門としては、画像識別アルゴリズム実験用の画像データセットとして公開されているMNISTデータセット(http://yann.lecun.com/exdb/mnist/)を使った画像識別が、いわゆるプログラミング言語のHello Worldに相当するものとされています。

ただし、二次元数値データの二値分類を深層学習で行い、その動作を確認してみることは、深層学習を始めるうえでのより簡単な一歩になると思います。深層学習の最初の一歩をここから始め、その後に画像識別や言語識別のような、より深層学習の力が発揮できる領域に入ってみてはいかがでしょうか。

ここでは深層学習の最初の一歩として、Microsoft Cognitive ToolkitのPython APIを使った順伝播型ネットワーク(feed forward network)による二値分類のチュートリアルを実行してみます。使用するチュートリアルは以下になります。

CNTK 102: Feed Forward Network with Simulated Data:
https://github.com/Microsoft/CNTK/blob/v2.0.rc2/Tutorials/CNTK_102_FeedForward.ipynb

シナリオ

被験者の年齢と腫瘍の大きさから、良性腫瘍と悪性腫瘍を深層学習にて分類します。データはプログラムで生成したシミュレーションデータとします。

必要なモジュールのインポート

以下のモジュールをインポートしておきます。なお、「%matplotlib inline」はJupyter Notebookを使用する場合にのみ必要です。

from __future__ import print_function
import matplotlib.pyplot as plt
%matplotlib inline

import numpy as np
import sys
import os

import cntk as C
from cntk import Trainer, learning_rate_schedule, UnitType, sgd
from cntk.initializer import glorot_uniform
from cntk.layers import default_options, Dense

デバイスの設定

プログラムを実行するデバイス(CPUもしくはGPU)を指定します。オプションとして、GPUをロックすることもできます(デフォルトはOFFです)。

if 'TEST_DEVICE' in os.environ:
    import cntk
    if os.environ['TEST_DEVICE'] == 'cpu':
        cntk.device.try_set_default_device(cntk.device.cpu())
    else:
        cntk.device.try_set_default_device(cntk.device.gpu(0))

シミュレーションデータの生成

二次元データの二値分類を行うため、特徴数(input_dim)として2、ラベル数(num_output_classes)として2を指定します。なお、同じ乱数を発生するようにseedを固定します。

np.random.seed(0)

input_dim = 2
num_output_classes = 2


シミュレーションデータを生成する関数を定義します。

def generate_random_data_sample(sample_size, feature_dim, num_classes): 
    Y = np.random.randint(size=(sample_size, 1), low=0, high=num_classes)

    X = (np.random.randn(sample_size, feature_dim)+3) * (Y+1)
    X = X.astype(np.float32)    

    class_ind = [Y==class_number for class_number in range(num_classes)]
    Y = np.asarray(np.hstack(class_ind), dtype=np.float32)

    return X, Y


サンプル数を64として、シミュレーションデータを生成します。

mysamplesize = 64
features, labels = generate_random_data_sample(mysamplesize, input_dim, num_output_classes)


シミュレーションデータを可視化します。X軸を被験者の年齢、Y軸を腫瘍の大きさとし、悪性腫瘍を赤点、良性腫瘍を青点としています。

colors = ['r' if l == 0 else 'b' for l in labels[:,0]]

plt.scatter(features[:,0], features[:,1], c=colors)
plt.xlabel("Scaled age (in yrs)")
plt.ylabel("Tumor size (in cm)")
plt.show()


ここまでのプログラムを実行すると、以下のようなグラフが表示されます。
f:id:masakykato:20170509185143p:plain

このプログラムにより、どのようなシミュレーションデータが生成されるかが把握できるかと思います。

順伝播型ネットワークモデルの作成

このチュートリアルでは、フルコネクトの順伝播型ネットワークを使用します。フルコネクトとは、下図のようにすべての隣接層のノードが接続された(つまり、前層のすべてのノードが次層の各ノードの入力になる)ネットワークのことであり、順伝播型とは情報が入力側から出力側に一方向にのみ伝播するネットワークのことです。

f:id:masakykato:20170510111801p:plain:w300


隠れ層の数(num_hidden_layers)を2、各隠れ層のノード数(hidden_layers_dim)を50とします。

num_hidden_layers = 2
hidden_layers_dim = 50


ネットワークへの入力変数(特徴やラベル)を定義します。Cognitive Toolkitでは、モデルの訓練やモデルのテストで使用する様々な観測値を、ネットワークへの入力変数に格納します。したがって、入力変数の次元は使用する訓練データの次元と一致します。訓練データは「被験者の年齢」と「腫瘍の大きさ」という次元を持つため、次元数は2になります。

input = C.input(input_dim)
label = C.input(num_output_classes)


ここからは順伝播型のニューラルネットワークモデルを作成していきます。

順伝播型ネットワークでは、n+1番目の層のノードの出力{ \displaystyle \boldsymbol{z^{(n+1)}}}はn番目の層のノードの出力{ \displaystyle \boldsymbol{z^{(n)}}}から
{ \displaystyle \boldsymbol{u^{(n+1)}=W^{(n+1)}z^{(n)}+b^{(n+1)}}}
{ \displaystyle \boldsymbol{z^{(n+1)}=f(u^{(n+1)})}}

で計算されます。ここで、{ \displaystyle \boldsymbol{W}}は重み、{ \displaystyle \boldsymbol{b}}はバイアス、{ \displaystyle \boldsymbol{f}}は活性化関数です。活性化関数としてはシグモイド関数や双曲線正接関数がよく使われます。

活性化関数としてシグモイド関数を使った場合、最終的な出力は{ \displaystyle \boldsymbol{u^{(n+1)}=W^{(n+1)}z^{(n)}+b^{(n+1)}}}として

def linear_layer(input_var, output_dim):
    input_dim = input_var.shape[0]
    
    weight = C.parameter(shape=(input_dim, output_dim))
    bias = C.parameter(shape=(output_dim))

    return bias + C.times(input_var, weight)


{ \displaystyle \boldsymbol{z^{(n+1)}=f(u^{(n+1)})}}として

def dense_layer(input_var, output_dim, nonlinearity):
    l = linear_layer(input_var, output_dim)
    
    return nonlinearity(l)


とすることにより、

def fully_connected_classifier_net(input_var, num_output_classes, hidden_layer_dim, 
                                   num_hidden_layers, nonlinearity):
    
    h = dense_layer(input_var, hidden_layer_dim, nonlinearity)
    for i in range(1, num_hidden_layers):
        h = dense_layer(h, hidden_layer_dim, nonlinearity)
    
    return linear_layer(h, num_output_classes)

z = fully_connected_classifier_net(input, num_output_classes, hidden_layers_dim, 
                                   num_hidden_layers, C.sigmoid)


と記述できます。

このネットワークモデルは、Cognitive ToolkitのLayer Libraryを使うと、以下のように、より簡単に記述できます。

def create_model(features):
    with default_options(init=glorot_uniform(), activation=C.sigmoid):
        h = features
        for _ in range(num_hidden_layers):
            h = Dense(hidden_layers_dim)(h)
        last_layer = Dense(num_output_classes, activation = None)
        
        return last_layer(h)
        
z = create_model(input)


ここでは、デフォルトのオプションで、重みとバイアスのイニシャライザとしてGlorotイニシャライザ(fanIn+fanOutでスケーリングした一様分布)を指定し、活性化関数としてシグモイド関数を指定しています。

ネットワークモデルの訓練の準備

順伝播型ネットワークモデルの訓練では、交差エントロピーを誤差関数とし、重み{ \displaystyle \boldsymbol{W}}とバイアス{ \displaystyle \boldsymbol{b}}に対して最小化させます。

交差エントロピーは、最終層の出力に対してソフトマックス関数で予測確率{ \displaystyle \boldsymbol{p}}を
{ \displaystyle \boldsymbol{p = softmax(z)}}

と定義することで、以下のように計算できます。
{ \displaystyle \boldsymbol{H(p)= - \displaystyle{\Sigma_{j=1}^{C}}y_i log(p_j)}}

ここで、{ \displaystyle \boldsymbol{C}}はラベルの次元数、{ \displaystyle \boldsymbol{y_i}}はラベルを表しています。

Cognitive Toolkitは交差エントロピーを計算するパッケージを持っているため、ネットワークの出力と訓練データのラベルを引数にして記述できます。

loss = C.cross_entropy_with_softmax(z, label)


同じく、ネットワークの出力に対する誤差も、ネットワークの出力と訓練データのラベルを引数にして記述できます。

eval_error = C.classification_error(z, label)


確率的勾配降下法(SGD: Stochastic Gradient Descent)は誤算関数を最小化させる最も一般的な手法です。ここではSGDを使用して、ネットワークモデルの訓練を行います。確率的勾配降下法では、重みとバイアスの初期値(ここではGlorotイニシャライザにより初期化)から始め、訓練データごとに予測されたラベル値と正しいラベル値に対する誤差関数を評価し、重みとバイアスの値を調整する処理を繰り返します。

このチュートリアルでは、個々の訓練データに対してではなく、より計算効率を高めるために、訓練データを特定のサンプル数でまとめたミニバッチに対してSGDを適用します。

SGDにおける重要なパラメータとして、学習率があります。これは誤差関数を最小化させる(数学的には極小解に収束させるという言い方をします)ために重要なパラメータです。この値が大きいとうまく収束できず、小さいと適切な極小解に収束できない、もしくは収束が遅くなるという性質を持つため、この値の調整は非常に重要です。

このチュートリアルでは0.5という値においています。

learning_rate = 0.5


Cognitive Toolkitでは、SGDを使った訓練オブジェクトを作成し、そのオブジェクトに対して訓練データを投入します。訓練オブジェクトは以下のように記述できます。

lr_schedule = C.learning_rate_schedule(learning_rate, UnitType.minibatch) 
learner = C.sgd(z.parameters, lr_schedule)
trainer = Trainer(z, (loss, eval_error), [learner])


その他、訓練の結果を可視化するために役立つ関数として、移動平均を計算する関数と、訓練の進捗を出力する関数を定義しておきます。

def moving_average(a, w=10):    
    if len(a) < w: 
        return a[:]    # Need to send a copy of the array
    return [val if idx < w else sum(a[(idx-w):idx])/w for idx, val in enumerate(a)]


def print_training_progress(trainer, mb, frequency, verbose=1):    
    training_loss = "NA"
    eval_error = "NA"

    if mb%frequency == 0:
        training_loss = trainer.previous_minibatch_loss_average
        eval_error = trainer.previous_minibatch_evaluation_average
        if verbose: 
            print ("Minibatch: {}, Train Loss: {}, Train Error: {}".format(mb, training_loss, eval_error))
        
    return mb, training_loss, eval_error

ネットワークモデルの訓練の実行

ミニバッチに含まれる訓練データ数(minibatch_size)、全訓練データ数(num_samples)を定義します。また、処理を行う回数(num_minibatches_to_train)も定義しておきます。

minibatch_size = 25
num_samples = 20000
num_minibatches_to_train = num_samples / minibatch_size


訓練を実行します。訓練データは、ミニバッチの大きさの訓練データを毎回プログラムで生成しています。

training_progress_output_freq = 20

plotdata = {"batchsize":[], "loss":[], "error":[]}

for i in range(0, int(num_minibatches_to_train)):
    features, labels = generate_random_data_sample(minibatch_size, input_dim, num_output_classes)
    
    # Specify the input variables mapping in the model to actual minibatch data for training
    trainer.train_minibatch({input : features, label : labels})
    batchsize, loss, error = print_training_progress(trainer, i, 
                                                     training_progress_output_freq, verbose=0)
    
    if not (loss == "NA" or error =="NA"):
        plotdata["batchsize"].append(batchsize)
        plotdata["loss"].append(loss)
        plotdata["error"].append(error)


訓練結果の可視化をします。1つ目のグラフでは、X軸を実行したミニバッチの件数、Y軸を誤差関数の値とし、2つ目のグラフではY軸を移動平均の値としています。

plotdata["avgloss"] = moving_average(plotdata["loss"])
plotdata["avgerror"] = moving_average(plotdata["error"])


plt.figure(1)
plt.subplot(211)
plt.plot(plotdata["batchsize"], plotdata["avgloss"], 'b--')
plt.xlabel('Minibatch number')
plt.ylabel('Loss')
plt.title('Minibatch run vs. Training loss')

plt.show()

plt.subplot(212)
plt.plot(plotdata["batchsize"], plotdata["avgerror"], 'r--')
plt.xlabel('Minibatch number')
plt.ylabel('Label Prediction Error')
plt.title('Minibatch run vs. Label Prediction Error')
plt.show()


ここまでのプログラムを実行すると、以下のようなグラフが表示されます。これを見ると、誤差関数、移動平均共に、実行したミニバッチの件数が増えるにしたがって収束していくことが分かるかと思います。

f:id:masakykato:20170517184156j:plain:w400

f:id:masakykato:20170517184205j:plain:w400

訓練済みネットワークモデルの評価

ネットワークモデルの訓練が完了しましたので、ここではテストデータを使い、訓練済みネットワークモデルを評価します。

テストデータも訓練データと同様に、プログラムで生成したシミュレーションデータとしています。

test_minibatch_size = 25
features, labels = generate_random_data_sample(test_minibatch_size, input_dim, num_output_classes)


訓練済みのネットワークモデルに対して、テストデータを投入します。

trainer.test_minibatch({input : features, label : labels})


ここまでのプログラムを実行すると、テストデータを使用した場合の誤差率が表示されます。

個々のテストデータに対する正誤を確認する場合には、以下のコードを記述して実行します。

out = C.softmax(z)

predicted_label_probs = out.eval({input : features})
print("Label    :", [np.argmax(label) for label in labels])
print("Predicted:", [np.argmax(row) for row in predicted_label_probs])


以上で、深層学習による二値分類のチュートリアルが終了しました。このチュートリアルをベースとして、学習率を変更した時の精度の変化や、確率的勾配効果法以外の手法を試してみるのもよいと思います。

Microsoft Translatorを使ったテキスト機械翻訳 －基本編

Microsoft Translatorは機械翻訳のためのSaaS APIです。現在はAzure Cognitive Servicesという人工知能サービスAPI群の一つとして提供されています。

以前はAzure DataMarketというサービスで提供されていましたが、DataMarketは2017年3月31日で提供終了、DataMarketでのMicrosoft Translatorへのアクセスも2017年4月30日で終了します。

このサービスはテキスト翻訳のためのTranslator Text APIと音声翻訳のためのTranslator Speech APIを提供していますが、ここではTranslator Text APIの特徴と基本的な使い方を紹介しようと思います。

特徴

  • クラウドベースのAPIとして提供されているため、様々なアプリケーションに容易に組み込むことが可能
  • Bing翻訳やOffice、Skype Translatorにも組み込まれており、アプリケーションとしてすぐ使えるものとしても提供している
  • 日本語を含む60言語 (2017年2月) に対応している

統計的機械翻訳は辞書登録だけで翻訳品質を上げることは難しく、対訳文 (日本語の文章と英語の文章のペアのような) で学習させることが必要と言われていますが、深層学習型機械翻訳は統計的機械翻訳よりもはるかに高い翻訳品質を実現するものとして期待されています。

まずは試してみる

Microsoft Translatorを簡単に試してみるには、Bing翻訳を使うのがてっとり早いです。「category」GETパラメータで「generalnn」と指定するだけで、アルゴリズムが切り替わります。

例としてMicrosoft Translatorの製品ページにある以下の文章を訳してみます。

Microsoft Translator Text API, part of the Microsoft Cognitive Services API collection, is a cloud-based machine translation service supporting multiple languages that reach more than 95% of world's gross domestic product (GDP). Translator can be used to build applications, websites, tools, or any solution requiring multilanguage support.


統計的機械翻訳の場合：
Microsoft Translator テキスト API、Microsoft 認知サービス API コレクションの一部は、世界の国内総生産 (GDP) の 95% 以上に達する複数の言語のサポート クラウド ベースの機械翻訳サービスです。アプリケーション、web サイト、ツール、または複数言語のサポートを必要とする任意のソリューションを構築するトランスレーターを使用することができます。

f:id:masakykato:20170214164711p:plain

個人目的として使う分にはよさそうですが、正式文書で使うには学習したほうがよさそうです。


深層学習型機械翻訳の場合：
microsoft 認知サービス api コレクションの一部である Microsoft Translator テキスト api は、世界の国内総生産 (gdp) の 95% 以上に達する複数の言語をサポートするクラウドベースの機械翻訳サービスです。トランスレータは、アプリケーション、web サイト、ツール、または多言語サポートを必要とする任意のソリューションを構築するために使用できます

f:id:masakykato:20170214165013p:plain

自然な文書になってますね。アルゴリズムを変えるだけで、ここまで訳に変化が出ています。

Translator Text APIを使ってみる

それでは本題であるTranslator Text APIの使い方を紹介していきます。Translator Text APIでもアルゴリズムの変更は簡単にできますので、合わせて紹介していきます。
なお、Translator Text APIにはREST、SOAP、AJAXの3つの種類のAPIがありますが、ここではREST APIを使用します。

Translator Text APIを使用するには、以下の3つの手順が必要になります。

  • Subscription Keyの取得
    • 認証トークンを取得するために必要になります。認証トークンの取得方法はAzure DataMarketで提供されていた時点のものから変更されていますので、ご注意ください。
  • 認証サービスの呼出
    • 認証サービスを呼び出し、Subscription Keyから認証トークンを生成します。
  • 翻訳サービスの呼出
    • 認証サービスを呼び出し、文章を翻訳します。

以下では、これらの基本的な使用方法について記述していきます。

Subscription Keyの取得

まずはAzureが使用できるようにしてください。こちらについては各種情報があると思いますので、そちらをご参考に。

Azureポータルにログインしたら、左のメニューから「新規」→「Intelligence + analytics」→「Cognitive Services APIs」を選択します。
f:id:masakykato:20170223175502p:plain

Cognitive Servicesアカウントの作成画面で、以下の項目を入力し、アカウントを作成します。

  • Account name：アカウントの表示名を入力
  • サブスクリプション：利用可能なサブスクリプションを選択
  • API Type：Translator Text API
  • 価格レベル：任意の価格レベル(F0を選択すると、200万文字まで利用可能な無料版となります)
  • Resource Group：任意で作成もしくは既存のリソースグループを選択
  • Resource group location：自分のいる場所に近いロケーションを選択

f:id:masakykato:20170223180853p:plain

アカウントが作成されたら、作成したアカウントを選択し、「Keys」メニューを選択して「KEY 1」を確認します。こちらがSubscription Keyになりますので、記録しておいてください。
f:id:masakykato:20170223180746p:plain

Subscription Keyの取得方法については、以下のドキュメントを参考にしてください。
https://www.microsoft.com/ja-jp/translator/getstarted.aspx

認証サービスの呼出

Translator Text APIの呼出は、認証トークンによる認証が必要です。認証トークンは複数の認証サービスの呼出に対して再利用できますが、有効時間は10分となっているため、認証サービスを呼び出す際には有効時間を考慮する必要があります。

認証トークンは、認証サービスに対して「Ocp-Apim-Subscription-Key」ヘッダーにSubscription Keyをセットしてリクエストするか、「Subscription-Key」GETパラメータにSubscription Keyをセットしてリクエストすることで取得できます。認証サービスのURLは以下になります。
認証サービス：https://api.cognitive.microsoft.com/sts/v1.0/issueToken


翻訳サービスの呼出時には、認証トークンをBearトークンとしてヘッダーにセットして渡します。


以下のコードは、認証サービスを呼び出すためのC#のサンプルクラスになります。

public class AzureAuthToken
    {
        // 認証サービスのURL
        private static readonly Uri ServiceUrl = new Uri("https://api.cognitive.microsoft.com/sts/v1.0/issueToken");
        // Subscription Keyを渡すときの要求ヘッダー
        private const string OcpApimSubscriptionKeyHeader = "Ocp-Apim-Subscription-Key";
        // 認証トークンの有効時間：5分
        private static readonly TimeSpan TokenCacheDuration = new TimeSpan(0, 5, 0);
        // 有効な認証トークンを格納
        private string storedTokenValue = string.Empty;
        // 有効な認証トークンの取得時間
        private DateTime storedTokenTime = DateTime.MinValue;

        /*
          Subscription Keyの取得
        */
        public string SubscriptionKey { get; private set; } = string.Empty;

        /*
         認証サービスへのリクエスト時のHTTPステータスコードの取得
        */
        public HttpStatusCode RequestStatusCode { get; private set; }

        /*
          認証トークンを取得するためのクライアント作成
          <param name="key">Subscription Key</param>
        */
        public AzureAuthToken(string key)
        {
            if (string.IsNullOrEmpty(key))
            {
                throw new ArgumentNullException("key", "Subscription Keyが必要です。");
            }

            this.SubscriptionKey = key;
            this.RequestStatusCode = HttpStatusCode.InternalServerError;
        }

        /*
          Subscriptionに紐づいた認証トークンの取得 (非同期)
        */
        public async Task<string> GetAccessTokenAsync()
        {
            if (SubscriptionKey == string.Empty) return string.Empty;

            // 認証トークンが有効な場合は有効な認証トークンを返す
            if ((DateTime.Now - storedTokenTime) < TokenCacheDuration)
            {
                return storedTokenValue;
            }

            // 認証トークンを取得
            using (var client = new HttpClient())
            using (var request = new HttpRequestMessage())
            {
                request.Method = HttpMethod.Post;
                request.RequestUri = ServiceUrl;
                request.Content = new StringContent(string.Empty);
                request.Headers.TryAddWithoutValidation(OcpApimSubscriptionKeyHeader, this.SubscriptionKey);
                client.Timeout = TimeSpan.FromSeconds(2);
                var response = await client.SendAsync(request);
                this.RequestStatusCode = response.StatusCode;
                response.EnsureSuccessStatusCode();
                var token = await response.Content.ReadAsStringAsync();
                storedTokenTime = DateTime.Now;
                storedTokenValue = "Bearer " + token;
                return storedTokenValue;
            }
        }

        /*
          Subscriptionに紐づいた認証トークンの取得 (同期)
        */
        public string GetAccessToken()
        {
            // 認証トークンが有効な場合は有効な認証トークンを返す
            if ((DateTime.Now - storedTokenTime) < TokenCacheDuration)
            {
                return storedTokenValue;
            }

            // 認証トークンを取得
            string accessToken = null;

            var task = Task.Run(async () =>
            {
                accessToken = await GetAccessTokenAsync();
            });

            while (!task.IsCompleted)
            {
                System.Threading.Thread.Yield();
            }

            if (task.IsFaulted)
            {
                throw task.Exception;
            }
            else if (task.IsCanceled)
            {
                throw new Exception("トークンの取得がタイムアウトしました。");
            }

            return accessToken;
        }
    }


認証サービスの使用方法については、以下のドキュメントを参考にしてください。
http://docs.microsofttranslator.com/oauth-token.html

翻訳サービスの呼出

翻訳サービスは
http://api.microsofttranslator.com/v2/Http.svc/
こちらのURLで提供されています。複数のサービスが使用できますが、最も単純な翻訳サービスは以下になります。
http://api.microsofttranslator.com/v2/http.svc/translate

このサービスに対して以下のGETパラメータを指定してリクエストすることで、翻訳が実行されます。

  • text
    • 翻訳対象文書
  • appId
  • from
    • 翻訳元言語
  • to
    • 翻訳先言語
  • category

以下のコードは、翻訳サービスを呼び出すためのC#のサンプルクラスになります。

public class CallTranslator
    {
        // Subscription Key
        private const string SubscriptionKey = "<Subscription Keyを入力>";
        // TranslateサービスのURL
        private static readonly Uri ServiceUrl = new Uri("http://api.microsofttranslator.com/v2/Http.svc/");

        /*
          翻訳の実施
          <param name="textToTransform">翻訳対象文書</param>
          <param name="fromLangCode">翻訳元言語</param>
          <param name="toLangCode">翻訳先言語</param>
          <param name="domain">翻訳ドメイン</param>
        */
        public string TranslateMethod(string textToTransform, string fromLangCode, string toLangCode, string domain)
        {
            // トークンの取得
            var authTokenSource = new AzureAuthToken(SubscriptionKey);
            var token = string.Empty;
            token = authTokenSource.GetAccessToken();

            // 翻訳サービスの呼出
            string uri = ServiceUrl + "Translate?text=" + System.Web.HttpUtility.UrlEncode(textToTransform) 
                + "&appid=" + token + "&from=" + fromLangCode + "&to=" + toLangCode + "&category=" + domain;
            HttpWebRequest httpWebRequest = (HttpWebRequest)WebRequest.Create(uri);
            WebResponse response = null;
            string translatedText = null;

            try
            {
                response = httpWebRequest.GetResponse();
                using (Stream stream = response.GetResponseStream())
                {
                    System.Runtime.Serialization.DataContractSerializer dcs = new System.Runtime.Serialization.DataContractSerializer(Type.GetType("System.String"));
                    translatedText = (string)dcs.ReadObject(stream);
                }
            } catch (Exception ex){
                Console.WriteLine("message: " + ex.Message);
                Console.WriteLine("stack trace: ");
                Console.WriteLine(ex.StackTrace);
                Console.ReadLine();
            }

            return translatedText;
        }


翻訳サービスの使用方法については、以下のドキュメントを参考にしてください。こちらではその他のサービスの使用方法についても記載されています。
http://docs.microsofttranslator.com/text-translate.html#!/default/get_Translate


上記のコードを使用したサンプルコードをGitHubで公開していますので、そちらも参考にしてみてください。サンプルコードでは、翻訳対象文書から翻訳元言語を自動識別するサービスも使っています。
https://github.com/masakykato0526/SimpleMicrosoftTranslator

私訳：NumPy Quickstart tutorial

機械学習 深層学習 Python NumPy

Pythonの数学計算ライブラリであるNumPyは深層学習を含めた機械学習に必須のライブラリですが、日本語情報があまり多くないため、Quickstart tutorialを翻訳してみました。

あくまで私訳ですので、原文と合わせてみて頂ければと思います。

原文：

https://docs.scipy.org/doc/numpy-dev/user/quickstart.html

前提

このチュートリアルを読む前に、Pythonについてある程度知っておいたほうがよいです。記憶を蘇らせたいのであれば、Python tutorial を参照してください。

このチュートリアルのサンプルを実行したい場合は、自分のコンピューターにソフトウエアをインストールしておく必要があります。手順については、http://scipy.org/install.htmlを参照してください。

基礎

NumPy の主要なオブジェクトは、同次の多次元配列です。これは(通常は数字の)要素のテーブルであり、全て同じ型、正の整数のタプルでインデックス付けされています。NumPyでは、次元は軸、軸の数はランクと呼ばれます。

例えば、三次元空間における点の座標「[1, 2, 1]」は、軸が1つであるためランク1の配列になります。軸の長さは3になります。以下の図の例では、配列はランク2 (2次元) となります。最初の次元 (軸) の長さは2、2つ目の次元の長さは3になります。

[[ 1., 0., 0.],
 [ 0., 1., 2.]] 

NumPyの配列クラスは「ndarray」と呼ばれています。これは「array」というエイリアスとしても知られています。標準のPythonライブラリの「array.array」クラスと同じではないということに注意してください。「array.array」クラスは一次元配列しか扱えませんし、機能も不足しています。「ndarray」クラスの重要な属性を以下に挙げておきます：

ndarray.ndim

配列の軸 (次元) 数です。Pythonの世界では、次元数はランクと呼ばれます。

ndarray.shape

配列に含まれる次元です。これは各次元の配列の大きさを表す整数のタプルになります。n行m列の行列の場合「shape」は「(n,m)」となります。「shape」タプルの長さはランクもしくは次元数である「ndim」の値となります。

ndarray.size

配列に含まれる要素の総数です。これは「shape」の要素の積と等しくなります。

ndarray.dtype

配列に含まれる要素の型を記述するオブジェクトです。dtypeは標準Pythonの型を用いて作成もしくは指定することができます。それに加えて、NumPyはnumpy.int32, numpy.int16, numpy.float64等の独自の型を提供しています。

ndarray.itemsize

配列に含まれる各要素のバイト単位の大きさです。例えば、「float64」型の要素からなる配列では、「itemsize」は8 (=64/8) となり、「complex32」型では4 (=32/8) となります。これはndarray.dtype.itemsizeと同値になります

ndarray.data

配列の実際の要素を収容しているバッファです。配列の要素にはインデックス機能を用いてアクセスするので、通常この属性を使う必要はないでしょう。

例

>>> import numpy as np
>>> a = np.arange(15).reshape(3, 5)
>>> a
array([[ 0,  1,  2,  3,  4],
       [ 5,  6,  7,  8,  9],
       [10, 11, 12, 13, 14]])
>>> a.shape
(3, 5)
>>> a.ndim
2
>>> a.dtype.name
'int64'
>>> a.itemsize
8
>>> a.size
15
>>> type(a)
<type 'numpy.ndarray'>
>>> b = np.array([6, 7, 8])
>>> b
array([6, 7, 8])
>>> type(b)
<type 'numpy.ndarray'>

配列の作成

配列を作成するには、何通りかの方法があります。

例えば、通常のPythonのリストや「array」関数を使用たタプルから配列を作成することができます。作成された配列の型は、シーケンスの要素の型から推定されます。

>>> import numpy as np
>>> a = np.array([2,3,4])
>>> a
array([2, 3, 4])
>>> a.dtype
dtype('int64')
>>> b = np.array([1.2, 3.5, 5.1])
>>> b.dtype
dtype('float64')

「array」関数を呼ぶときに、引数として一つの数値のリストを渡すのでなく複数の数値の引数を渡してエラーになるというのは、よくある間違いです。

>>> a = np.array(1,2,3,4)    # WRONG
>>> a = np.array([1,2,3,4])  # RIGHT

「array」は、シーケンスのシーケンスを2次元配列に、シーケンスのシーケンスのシーケンスを3次元配列に、といった形で変換します。

>>> b = np.array([(1.5,2,3), (4,5,6)])
>>> b
array([[ 1.5,  2. ,  3. ],
       [ 4. ,  5. ,  6. ]])

 配列の作成時に、明示的に型を指定することもできます：

>>> c = np.array( [ [1,2], [3,4] ], dtype=complex )
>>> c
array([[ 1.+0.j,  2.+0.j],
       [ 3.+0.j,  4.+0.j]])

配列の要素が最初は分からず、大きさだけが分かっているということはよくあることです。そのためNumPyは、場所取り用の初期値を入れて配列を作成する関数を提供しています。これにより、コストのかかる演算である配列の拡張の必要性を最小限に抑えられます。

「zeros」関数はすべて0の値を持つ配列を、「ones」関数はすべて1の値を持つ配列を、「empty」はメモリ状態に依存したランダムな初期値を持つ配列を作成します。デフォルトでは、作成された配列のdtypeは「float64」になります。

>>> np.zeros( (3,4) )
array([[ 0.,  0.,  0.,  0.],
       [ 0.,  0.,  0.,  0.],
       [ 0.,  0.,  0.,  0.]])
>>> np.ones( (2,3,4), dtype=np.int16 )                # dtype can also be specified
array([[[ 1, 1, 1, 1],
        [ 1, 1, 1, 1],
        [ 1, 1, 1, 1]],
       [[ 1, 1, 1, 1],
        [ 1, 1, 1, 1],
        [ 1, 1, 1, 1]]], dtype=int16)
>>> np.empty( (2,3) )                                 # uninitialized, output may vary
array([[  3.73603959e-262,   6.02658058e-154,   6.55490914e-260],
       [  5.30498948e-313,   3.14673309e-307,   1.00000000e+000]])

数値のシーケンスを作成するために、NumPyは、「range」に似た、リストの代わりに配列を返す関数を提供しています。

>>> np.arange( 10, 30, 5 )
array([10, 15, 20, 25])
>>> np.arange( 0, 2, 0.3 )                 # it accepts float arguments
array([ 0. ,  0.3,  0.6,  0.9,  1.2,  1.5,  1.8])

「arange」が浮動小数点数を引数として使用する場合、浮動小数の精度が有限であるために、一般的には得られる要素数を予測することはできません。このため、stepの代わりに必要な要素数を引数として渡せる「linespace」関数を使うほうが通常望ましいです：

>>> from numpy import pi
>>> np.linspace( 0, 2, 9 )                 # 9 numbers from 0 to 2
array([ 0.  ,  0.25,  0.5 ,  0.75,  1.  ,  1.25,  1.5 ,  1.75,  2.  ])
>>> x = np.linspace( 0, 2*pi, 100 )        # useful to evaluate function at lots of points
>>> f = np.sin(x)
関連項目

array, zeros, zeros_like, ones, ones_like, empty, empty_like, arange, linspace, numpy.random.rand, numpy.random.randn, fromfunction,fromfile 

配列の表示

配列を表示する時、NumPyはネストされたリストと同じような方法で表示しますが、以下のレイアウトになります：

  • 最後の軸は左から右へ表示されます。
  • 最後から2番目の軸は、上から下へ表示されます。
  • その他の軸も上から下へ表示されますが、各スライスは空行で区切られます。

したがって、1次元配列は行のように、2次元配列は行列のように、3次元配列は行列のリストのように表示されます。

>>> a = np.arange(6)                         # 1d array
>>> print(a)
[0 1 2 3 4 5]
>>>
>>> b = np.arange(12).reshape(4,3)           # 2d array
>>> print(b)
[[ 0  1  2]
 [ 3  4  5]
 [ 6  7  8]
 [ 9 10 11]]
>>>
>>> c = np.arange(24).reshape(2,3,4)         # 3d array
>>> print(c)
[[[ 0  1  2  3]
  [ 4  5  6  7]
  [ 8  9 10 11]]
 [[12 13 14 15]
  [16 17 18 19]
  [20 21 22 23]]]

「reshape」の詳細については、「形状の操作」の項目を参照してください。

配列が大きすぎて表示できない場合には、NumPyは自動的に配列の中心部分を省略して端部分のみ表示します。

>>> print(np.arange(10000))
[   0    1    2 ..., 9997 9998 9999]
>>>
>>> print(np.arange(10000).reshape(100,100))
[[   0    1    2 ...,   97   98   99]
 [ 100  101  102 ...,  197  198  199]
 [ 200  201  202 ...,  297  298  299]
 ...,
 [9700 9701 9702 ..., 9797 9798 9799]
 [9800 9801 9802 ..., 9897 9898 9899]
 [9900 9901 9902 ..., 9997 9998 9999]]

この動作を無効にしてNumPyに配列全体を表示させたい場合には、「set_printoptions」を使用して表示オプションを変更することができます。

>>> np.set_printoptions(threshold='nan')

基本的な演算

配列に対する算術演算は要素ごとに適用されます。新しい配列が作成され、演算結果が入力されます。

>>> a = np.array( [20,30,40,50] )
>>> b = np.arange( 4 )
>>> b
array([0, 1, 2, 3])
>>> c = a-b
>>> c
array([20, 29, 38, 47])
>>> b**2
array([0, 1, 4, 9])
>>> 10*np.sin(a)
array([ 9.12945251, -9.88031624,  7.4511316 , -2.62374854])
>>> a<35
array([ True, True, False, False], dtype=bool)

多くの行列言語と異なり、NumPyでは乗算演算子「*」は要素ごとの演算を行います。行列の積は「dot」関数もしくはメソッドを使用して実行することができます：

>>> A = np.array( [[1,1],
...             [0,1]] )
>>> B = np.array( [[2,0],
...             [3,4]] )
>>> A*B                         # elementwise product
array([[2, 0],
       [0, 4]])
>>> A.dot(B)                    # matrix product
array([[5, 4],
       [3, 4]])
>>> np.dot(A, B)                # another matrix product
array([[5, 4],
       [3, 4]])

「+=」や「*=」のようないくつかの演算では、新しい行列を作成せずに、既存の配列を変更します。

>>> a = np.ones((2,3), dtype=int)
>>> b = np.random.random((2,3))
>>> a *= 3
>>> a
array([[3, 3, 3],
       [3, 3, 3]])
>>> b += a
>>> b
array([[ 3.417022  ,  3.72032449,  3.00011437],
       [ 3.30233257,  3.14675589,  3.09233859]])
>>> a += b                  # b is not automatically converted to integer type
Traceback (most recent call last):
  ...
TypeError: Cannot cast ufunc add output from dtype('float64') to dtype('int64') with casting rule 'same_kind'

 型が異なる行列に対して演算する場合、演算結果の配列の型は、より一般度の高い型もしくはより精度の高い型(アップキャストとして知られている動作)になります。

>>> a = np.ones(3, dtype=np.int32)
>>> b = np.linspace(0,pi,3)
>>> b.dtype.name
'float64'
>>> c = a+b
>>> c
array([ 1.        ,  2.57079633,  4.14159265])
>>> c.dtype.name
'float64'
>>> d = np.exp(c*1j)
>>> d
array([ 0.54030231+0.84147098j, -0.84147098+0.54030231j,
       -0.54030231-0.84147098j])
>>> d.dtype.name
'complex128'

配列に含まれる全要素の合計計算のような単項演算子の多くは、「ndarray」クラスのメソッドとして実装されています。

>>> a = np.random.random((2,3))
>>> a
array([[ 0.18626021,  0.34556073,  0.39676747],
       [ 0.53881673,  0.41919451,  0.6852195 ]])
>>> a.sum()
2.5718191614547998
>>> a.min()
0.1862602113776709
>>> a.max()
0.6852195003967595

これらの演算子は、デフォルトでは配列の形状にかかわらず、数値のリストのように配列に適用されます。しかし、「axis」パラメータを指定することで、指定された配列の軸に沿って演算を実施することができます：

>>> b = np.arange(12).reshape(3,4)
>>> b
array([[ 0,  1,  2,  3],
       [ 4,  5,  6,  7],
       [ 8,  9, 10, 11]])
>>>
>>> b.sum(axis=0)                            # sum of each column
array([12, 15, 18, 21])
>>>
>>> b.min(axis=1)                            # min of each row
array([0, 4, 8])
>>>
>>> b.cumsum(axis=1)                         # cumulative sum along each row
array([[ 0,  1,  3,  6],
       [ 4,  9, 15, 22],
       [ 8, 17, 27, 38]])

ユニバーサル関数

NumPyは、sin、cos、expのようなよく知られている数学関数も提供しています。NumPyでは、これらは「ユニバーサル関数(ufunc)」と呼ばれています。Numpyでは、これらの関数は配列の要素ごとに演算を行い、出力として新規の行列が作成されます。

>>> B = np.arange(3)
>>> B
array([0, 1, 2])
>>> np.exp(B)
array([ 1.        ,  2.71828183,  7.3890561 ])
>>> np.sqrt(B)
array([ 0.        ,  1.        ,  1.41421356])
>>> C = np.array([2., -1., 4.])
>>> np.add(B, C)
array([ 2.,  0.,  6.])
関連項目

all, any, apply_along_axis, argmax, argmin, argsort, average, bincount, ceil, clip, conj, corrcoef, cov, cross, cumprod, cumsum, diff,dot, floor, inner, inv, lexsort, max, maximum, mean, median, min, minimum, nonzero, outer, prod, re, round, sort, std, sum, trace,transpose, var, vdot, vectorize, where

インデックス付け、スライス、イテレート

一次元配列に対しては、リストや他のPythonのシーケンスと同じように、インデックス付けやスライス、イテレートを行うことができます。

>>> a = np.arange(10)**3
>>> a
array([  0,   1,   8,  27,  64, 125, 216, 343, 512, 729])
>>> a[2]
8
>>> a[2:5]
array([ 8, 27, 64])
>>> a[:6:2] = -1000    # equivalent to a[0:6:2] = -1000; from start to position 6, exclusive, set every 2nd element to -1000
>>> a
array([-1000,     1, -1000,    27, -1000,   125,   216,   343,   512,   729])
>>> a[ : :-1]                                 # reversed a
array([  729,   512,   343,   216,   125, -1000,    27, -1000,     1, -1000])
>>> for i in a:
...     print(i**(1/3.))
...
nan
1.0
nan
3.0
nan
5.0
6.0
7.0
8.0
9.0

多次元配列は、軸ごとに一つのインデックスを持つことができます。これらのインデックスは、カンマ区切りのタプルで与えられます：

>>> def f(x,y):
...     return 10*x+y
...
>>> b = np.fromfunction(f,(5,4),dtype=int)
>>> b
array([[ 0,  1,  2,  3],
       [10, 11, 12, 13],
       [20, 21, 22, 23],
       [30, 31, 32, 33],
       [40, 41, 42, 43]])
>>> b[2,3]
23
>>> b[0:5, 1]                       # each row in the second column of b
array([ 1, 11, 21, 31, 41])
>>> b[ : ,1]                        # equivalent to the previous example
array([ 1, 11, 21, 31, 41])
>>> b[1:3, : ]                      # each column in the second and third row of b
array([[10, 11, 12, 13],
       [20, 21, 22, 23]])

軸数より少ないインデックスが与えられた場合には、不足分のインデックスは完全なスライス「:」と見なされます。

>>> b[-1]                                  # the last row. Equivalent to b[-1,:]
array([40, 41, 42, 43])

「b[i]」の括弧の中の式は、残りの軸を表現するために必要な分の「:」で埋められているものとして扱われます。NumPyでは、これを「b[i,...]」のようにドットを用いて記述することもできます。

ドット「...」は、完全にインデックス付けされたタプルを生成するのに必要な分のコロンを表しています。例えば、「x」がランク5の配列(つまり5軸)の場合、以下の配列は等価になります。

  • x[1,2,...]はx[1,2,:,:,:]
  • x[...,3]はx[:,:,:,:,3]
  • x[4,...,5,:]はx[4,:,:,5,:]
>>> c = np.array( [[[  0,  1,  2],               # a 3D array (two stacked 2D arrays)
...                 [ 10, 12, 13]],
...                [[100,101,102],
...                 [110,112,113]]])
>>> c.shape
(2, 2, 3)
>>> c[1,...]                                   # same as c[1,:,:] or c[1]
array([[100, 101, 102],
       [110, 112, 113]])
>>> c[...,2]                                   # same as c[:,:,2]
array([[  2,  13],
       [102, 113]])

多次元配列に対するイテレートは、最初の軸に対して行われます：

>>> for row in b:
...     print(row)
...
[0 1 2 3]
[10 11 12 13]
[20 21 22 23]
[30 31 32 33]
[40 41 42 43]

一方で、配列の各要素に対して演算を行いたい場合には、配列の全要素に対して適用されるイテレータとなる「flat」属性を使用することができます：

>>> for element in b.flat:
...     print(element)
...
0
1
2
3
10
11
12
13
20
21
22
23
30
31
32
33
40
41
42
43
関連項目

Indexing, Indexing (reference), newaxis, ndenumerate, indices

形状の操作

配列の形状の変更

配列は、各軸に沿った要素数によって与えられる形状を持ちます：

>>> a = np.floor(10*np.random.random((3,4)))
>>> a
array([[ 2.,  8.,  0.,  6.],
       [ 4.,  5.,  1.,  1.],
       [ 8.,  9.,  3.,  6.]])
>>> a.shape
(3, 4)

配列の形状は、様々なコマンドで変更することができます：

>>> a.ravel()  # returns the array, flattened
array([ 2.,  8.,  0.,  6.,  4.,  5.,  1.,  1.,  8.,  9.,  3.,  6.])
>>> a.reshape(6,2)  # returns the array with a modified shape
array([[ 2.,  8.],
       [ 0.,  6.],
       [ 4.,  5.],
       [ 1.,  1.],
       [ 8.,  9.],
       [ 3.,  6.]])
>>> a.T  # returns the array, transposed
array([[ 2.,  4.,  8.],
       [ 8.,  5.,  9.],
       [ 0.,  1.,  3.],
       [ 6.,  1.,  6.]])
>>> a.T.shape
(4, 3)
>>> a.shape
(3, 4)

ravel()の結果として得られる配列の要素の順番は、通常は”Cスタイル”つまり一番右のインデックスが”最初の変わる”ので、a[0,0]の次の要素がa[0,1]になります。配列が別の形状に再整形されても、配列は"Cスタイル"として扱われます。NumPyは、通常はこの順番で格納される配列を作成するため、ravel()は普通は引数をコピーする必要がありませんが、配列が別の配列をスライスして作成されたり、一般的ではないオプションを使って作成された場合には、引数をコピーする必要があることがあります。ravel()とreshape() 関数 は、オプションの引数を使うことでFORTRANスタイルの配列、つまり一番左のインデックスが最初に変わるように指定することもできます。

reshape関数は、変更後の形状で引数を返す一方で、ndarray.resizeメソッドは配列そのものを変更します：

>>> a
array([[ 2.,  8.,  0.,  6.],
       [ 4.,  5.,  1.,  1.],
       [ 8.,  9.,  3.,  6.]])
>>> a.resize((2,6))
>>> a
array([[ 2.,  8.,  0.,  6.,  4.,  5.],
       [ 1.,  1.,  8.,  9.,  3.,  6.]])

再整形の演算時に次元が-1で与えられた場合、他の次元は自動的に計算されます。

>>> a.reshape(3,-1)
array([[ 2.,  8.,  0.,  6.],
       [ 4.,  5.,  1.,  1.],
       [ 8.,  9.,  3.,  6.]])
関連項目

ndarray.shape, reshape, resize, ravel

配列の積み上げ

複数の配列を、さまざまな軸に沿って積み上げることができます：

>>> a = np.floor(10*np.random.random((2,2)))
>>> a
array([[ 8.,  8.],
       [ 0.,  0.]])
>>> b = np.floor(10*np.random.random((2,2)))
>>> b
array([[ 1.,  8.],
       [ 0.,  4.]])
>>> np.vstack((a,b))
array([[ 8.,  8.],
       [ 0.,  0.],
       [ 1.,  8.],
       [ 0.,  4.]])
>>> np.hstack((a,b))
array([[ 8.,  8.,  1.,  8.],
       [ 0.,  0.,  0.,  4.]])

column_stack関数は、1次元配列を2次元配列に積み上げます。1次元配列の場合は、vstackと等価になります：

>>> from numpy import newaxis
>>> np.column_stack((a,b))   # With 2D arrays
array([[ 8.,  8.,  1.,  8.],
       [ 0.,  0.,  0.,  4.]])
>>> a = np.array([4.,2.])
>>> b = np.array([2.,8.])
>>> a[:,newaxis]  # This allows to have a 2D columns vector
array([[ 4.],
       [ 2.]])
>>> np.column_stack((a[:,newaxis],b[:,newaxis]))
array([[ 4.,  2.],
       [ 2.,  8.]])
>>> np.vstack((a[:,newaxis],b[:,newaxis])) # The behavior of vstack is different
array([[ 4.],
       [ 2.],
       [ 2.],
       [ 8.]])

2次元以上の配列の場合には、hstackは2つ目の軸に沿って積み上げ、vstackは最初の軸に沿って積み上げます。concatenateは連結する軸の番号をオプションの引数として指定することができます。

注釈

複雑な場合においては、ある軸に沿って数字を積み上げることで配列を作成するr_とc_が役に立ちます。これは、範囲を表すリテラルである「:」を使うことができます：

>>> np.r_[1:4,0,4]
array([1, 2, 3, 0, 4])

配列を引数として使う場合、r_とc_はvstackとhstackのデフォルトの動作に似てますが、連結する軸の番号をオプションの引数として指定することができます。

関連項目

hstack, vstack, column_stack, concatenate, c_, r_

配列を複数の小さな配列に分割

hsplitを使用すると、同じ形状の配列を返す数を指定することで、もしくは分割させる後ろの列を指定することで、配列を水平軸に沿って分割することができます：

>>> a = np.floor(10*np.random.random((2,12)))
>>> a
array([[ 9.,  5.,  6.,  3.,  6.,  8.,  0.,  7.,  9.,  7.,  2.,  7.],
       [ 1.,  4.,  9.,  2.,  2.,  1.,  0.,  6.,  2.,  2.,  4.,  0.]])
>>> np.hsplit(a,3)   # Split a into 3
[array([[ 9.,  5.,  6.,  3.],
       [ 1.,  4.,  9.,  2.]]), array([[ 6.,  8.,  0.,  7.],
       [ 2.,  1.,  0.,  6.]]), array([[ 9.,  7.,  2.,  7.],
       [ 2.,  2.,  4.,  0.]])]
>>> np.hsplit(a,(3,4))   # Split a after the third and the fourth column
[array([[ 9.,  5.,  6.],
       [ 1.,  4.,  9.]]), array([[ 3.],
       [ 2.]]), array([[ 6.,  8.,  0.,  7.,  9.,  7.,  2.,  7.],
       [ 2.,  1.,  0.,  6.,  2.,  2.,  4.,  0.]])]

vsplitは垂直軸に沿って分割し、array_splitはどの軸に沿って分割するかを指定することができます。

コピーとビュー

配列の演算や操作時には、データを新しい配列にコピーする場合もありますし、コピーしない場合もあります。これは時として初心者を混乱させる元となります。これには3つのケースがあります：

コピー無し

単純な代入では、配列オブジェクトもデータもコピーされません。

>>> a = np.arange(12)
>>> b = a            # no new object is created
>>> b is a           # a and b are two names for the same ndarray object
True
>>> b.shape = 3,4    # changes the shape of a
>>> a.shape
(3, 4)

Pythonは変更可能なオブジェクトを参照渡しするため、関数呼び出しではコピーは行いません。

>>> def f(x):
...     print(id(x))
...
>>> id(a)                           # id is a unique identifier of an object
148293216
>>> f(a)
148293216

ビューとシャローコピー

異なる配列オブジェクトが、同じデータを共有することができます。「view」メソッドは、同じデータを参照する新しい配列オブジェクトを作成します。

>>> c = a.view()
>>> c is a
False
>>> c.base is a                        # c is a view of the data owned by a
True
>>> c.flags.owndata
False
>>>
>>> c.shape = 2,6                      # a's shape doesn't change
>>> a.shape
(3, 4)
>>> c[0,4] = 1234                      # a's data changes
>>> a
array([[   0,    1,    2,    3],
       [1234,    5,    6,    7],
       [   8,    9,   10,   11]])

配列をスライスすると、ビューが返されます：

>>> s = a[ : , 1:3]     # spaces added for clarity; could also be written "s = a[:,1:3]"
>>> s[:] = 10           # s[:] is a view of s. Note the difference between s=10 and s[:]=10
>>> a
array([[   0,   10,   10,    3],
       [1234,   10,   10,    7],
       [   8,   10,   10,   11]])

ディープコピー

「copy」メソッドは、配列とそのデータの完全なコピーを作ります。

>>> d = a.copy()                          # a new array object with new data is created
>>> d is a
False
>>> d.base is a                           # d doesn't share anything with a
False
>>> d[0,0] = 9999
>>> a
array([[   0,   10,   10,    3],
       [1234,   10,   10,    7],
       [   8,   10,   10,   11]])

関数とメソッド概要

ここでは、役に立つNumPyの関数とメソッドをカテゴリ順にリストします。完全なリストはhttps://docs.scipy.org/doc/numpy-dev/reference/routines.html#routinesを参照してください。

Array Creation

arange, array, copy, empty, empty_like, eye, fromfile, fromfunction, identity, linspace, logspace, mgrid, ogrid, ones, ones_like, r,zeros, zeros_like

Conversions

ndarray.astype, atleast_1d, atleast_2d, atleast_3d, mat

Manipulations

array_split, column_stack, concatenate, diagonal, dsplit, dstack, hsplit, hstack, ndarray.item, newaxis, ravel, repeat, reshape,resize, squeeze, swapaxes, take, transpose, vsplit, vstack

Questions

all, any, nonzero, where

Ordering

argmax, argmin, argsort, max, min, ptp, searchsorted, sort

Operations

choose, compress, cumprod, cumsum, inner, ndarray.fill, imag, prod, put, putmask, real, sum

Basic Statistics

cov, mean, std, var

Basic Linear Algebra

cross, dot, outer, linalg.svd, vdot

応用

ブロードキャストルール

ブロードキャストにより、ユニバーサル関数は、正確には同じ形状ではない入力でも意味のある方法で扱うことができます。

ブロードキャストの1つ目のルールは、すべての入力は配列が同じ次元数を持たない場合、すべての配列が同じ次元数を持つまで、配列の先頭に「1」を穴埋めするものです。

ブロードキャストの2つ目のルールでは、特定の次元に沿った大きさが1である配列は、その次元に沿って最大の形状を持つ配列の大きさを持つものとして振舞うことを保証します。配列の要素の値は、「ブロードキャスト」配列の次元に沿って同じ値であるとみなされます。

ブロードキャストルールが適用されると、すべての配列の大きさは一致することになります。詳細は https://docs.scipy.org/doc/numpy-dev/user/basics.broadcasting.htmlに記載されています。

役に立つインデックス付けとインデックスのコツ

NumPyは、通常のPythonシーケンスよりも多くのインデックス機能を提供しています。整数やスライスによるインデックス付けに加えて、これまでに見てきたように、整数配列やブーリアン配列でも配列にインデックス付けすることができます。

インデックス配列によるインデックス付け

>>> a = np.arange(12)**2                       # the first 12 square numbers
>>> i = np.array( [ 1,1,3,8,5 ] )              # an array of indices
>>> a[i]                                       # the elements of a at the positions i
array([ 1,  1,  9, 64, 25])
>>>
>>> j = np.array( [ [ 3, 4], [ 9, 7 ] ] )      # a bidimensional array of indices
>>> a[j]                                       # the same shape as j
array([[ 9, 16],
       [81, 49]])

インデックス配列「a」が多次元配列の時、単一配列のインデックスは「a」の最初の次元を参照します。以下の例は、ラベルの画像をパレットを用いてカラー画像に変換することでこの振る舞いを表します。

>>> palette = np.array( [ [0,0,0],                # black
...                       [255,0,0],              # red
...                       [0,255,0],              # green
...                       [0,0,255],              # blue
...                       [255,255,255] ] )       # white
>>> image = np.array( [ [ 0, 1, 2, 0 ],           # each value corresponds to a color in the palette
...                     [ 0, 3, 4, 0 ]  ] )
>>> palette[image]                            # the (2,4,3) color image
array([[[  0,   0,   0],
        [255,   0,   0],
        [  0, 255,   0],
        [  0,   0,   0]],
       [[  0,   0,   0],
        [  0,   0, 255],
        [255, 255, 255],
        [  0,   0,   0]]])

1次元以上の配列に対してインデックスを与えることもできます。各次元に対するインデックス配列は、同じ形状である必要があります。

>>> a = np.arange(12).reshape(3,4)
>>> a
array([[ 0,  1,  2,  3],
       [ 4,  5,  6,  7],
       [ 8,  9, 10, 11]])
>>> i = np.array( [ [0,1],                        # indices for the first dim of a
...                 [1,2] ] )
>>> j = np.array( [ [2,1],                        # indices for the second dim
...                 [3,3] ] )
>>>
>>> a[i,j]                                     # i and j must have equal shape
array([[ 2,  5],
       [ 7, 11]])
>>>
>>> a[i,2]
array([[ 2,  6],
       [ 6, 10]])
>>>
>>> a[:,j]                                     # i.e., a[ : , j]
array([[[ 2,  1],
        [ 3,  3]],
       [[ 6,  5],
        [ 7,  7]],
       [[10,  9],
        [11, 11]]])

通常は、「i」と「j」をシーケンス (つまりリスト) に入れて、リストでインデックス付けを行います。

>>> l = [i,j]
>>> a[l]                                       # equivalent to a[i,j]
array([[ 2,  5],
       [ 7, 11]])

しかし、「i」と「j」を配列に入れると、同じことはできません。なぜならこの配列は、「a」の最初の次元をインデックス付けするものとして解釈されるからです。

>>> s = np.array( [i,j] )
>>> a[s]                                       # not what we want
Traceback (most recent call last):
  File "<stdin>", line 1, in ?
IndexError: index (3) out of range (0<=index<=2) in dimension 0
>>>
>>> a[tuple(s)]                                # same as a[i,j]
array([[ 2,  5],
       [ 7, 11]])

配列でインデックス付けする他のよくある使い方は、時間依存連続データの最大値検索です。

>>> time = np.linspace(20, 145, 5)                 # time scale
>>> data = np.sin(np.arange(20)).reshape(5,4)      # 4 time-dependent series
>>> time
array([  20.  ,   51.25,   82.5 ,  113.75,  145.  ])
>>> data
array([[ 0.        ,  0.84147098,  0.90929743,  0.14112001],
       [-0.7568025 , -0.95892427, -0.2794155 ,  0.6569866 ],
       [ 0.98935825,  0.41211849, -0.54402111, -0.99999021],
       [-0.53657292,  0.42016704,  0.99060736,  0.65028784],
       [-0.28790332, -0.96139749, -0.75098725,  0.14987721]])
>>>
>>> ind = data.argmax(axis=0)                   # index of the maxima for each series
>>> ind
array([2, 0, 3, 1])
>>>
>>> time_max = time[ ind]                       # times corresponding to the maxima
>>>
>>> data_max = data[ind, xrange(data.shape[1])] # => data[ind[0],0], data[ind[1],1]...
>>>
>>> time_max
array([  82.5 ,   20.  ,  113.75,   51.25])
>>> data_max
array([ 0.98935825,  0.84147098,  0.99060736,  0.6569866 ])
>>>
>>> np.all(data_max == data.max(axis=0))
True

代入する対象として、配列でインデックス付けすることにも使用できます。

>>> a = np.arange(5)
>>> a
array([0, 1, 2, 3, 4])
>>> a[[1,3,4]] = 0
>>> a
array([0, 0, 2, 0, 0])

一方で、インデックスのリストに繰り返しが含まれている場合、代入は複数回行われ、最後の値が残ります：

>>> a = np.arange(5)
>>> a[[0,0,2]]=[1,2,3]
>>> a
array([2, 1, 3, 3, 4])

これは十分に合理的なのですが、Pythonの「+=」構造を使いたいのであれば、期待している動作とは異なる場合があるので注意してください：

>>> a = np.arange(5)
>>> a[[0,0,2]]+=1
>>> a
array([1, 1, 3, 3, 4])

インデックスのリストに0が2回現れていますが、0番目の要素は1度しか増分されていません。これは、Pythonが「a+=1」を「a=a+1」と等価であるとしているためです。

ブール型配列によるインデックス付け

(整数の) インデックス配列で配列をインデックス付けする場合には、使用したいインデックスのリストを用意しています。ブール型インデックスを使う場合には、アプローチは異なります；使用したい配列の要素と使用したくない配列の要素を、明示的に選択します。

ブール型インデックス付けを検討する最もよくある方法は、元の配列と同じ形状を持つブール型配列を使うことです：

>>> a = np.arange(12).reshape(3,4)
>>> b = a > 4
>>> b                                          # b is a boolean with a's shape
array([[False, False, False, False],
       [False,  True,  True,  True],
       [ True,  True,  True,  True]], dtype=bool)
>>> a[b]                                       # 1d array with the selected elements
array([ 5,  6,  7,  8,  9, 10, 11])

この性質は、代入のときに非常に便利です：

>>> a[b] = 0                                   # All elements of 'a' higher than 4 become 0
>>> a
array([[0, 1, 2, 3],
       [4, 0, 0, 0],
       [0, 0, 0, 0]])

以下の例を見ると、「マンデルブロ集合」のイメージを生成するためにブール型インデックス付けをどのように使うかがわかります：

>>> import numpy as np
>>> import matplotlib.pyplot as plt
>>> def mandelbrot( h,w, maxit=20 ):
...     """Returns an image of the Mandelbrot fractal of size (h,w)."""
...     y,x = np.ogrid[ -1.4:1.4:h*1j, -2:0.8:w*1j ]
...     c = x+y*1j
...     z = c
...     divtime = maxit + np.zeros(z.shape, dtype=int)
...
...     for i in range(maxit):
...         z = z**2 + c
...         diverge = z*np.conj(z) > 2**2            # who is diverging
...         div_now = diverge & (divtime==maxit)  # who is diverging now
...         divtime[div_now] = i                  # note when
...         z[diverge] = 2                        # avoid diverging too much
...
...     return divtime
>>> plt.imshow(mandelbrot(400,400))
>>> plt.show()

f:id:masakykato:20170202200535p:plain

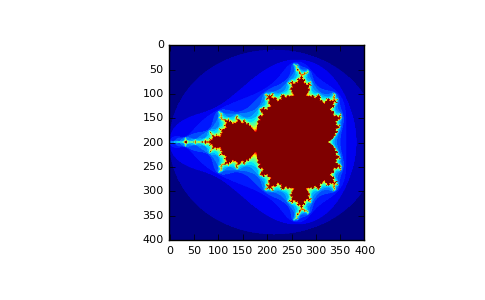
ブール型インデックス付けを使う2つ目の方法は、整数型インデックス付けにより似ています；配列の各次元に対して、欲しいスライスを選択して1次元のブール型配列を得ます。

>>> a = np.arange(12).reshape(3,4)
>>> b1 = np.array([False,True,True])             # first dim selection
>>> b2 = np.array([True,False,True,False])       # second dim selection
>>>
>>> a[b1,:]                                   # selecting rows
array([[ 4,  5,  6,  7],
       [ 8,  9, 10, 11]])
>>>
>>> a[b1]                                     # same thing
array([[ 4,  5,  6,  7],
       [ 8,  9, 10, 11]])
>>>
>>> a[:,b2]                                   # selecting columns
array([[ 0,  2],
       [ 4,  6],
       [ 8, 10]])
>>>
>>> a[b1,b2]                                  # a weird thing to do
array([ 4, 10])

1次元ブール型配列の長さはスライスしたい次元(もしくは軸)の長さと一致している必要があることに注意してください。前の例では、「b1」は長さが3 (「a」の行数) のランク1配列で、「b2」(長さが4) は「a」の2番目のランク(列)のインデックスに一致しています。

ix_()関数

「ix_」関数は、異なるベクトルを結合して各n-upletの結果を得るために使用することができます。例えば、ベクトルa、b、cから取得したすべての3つ組の値に対してa+b*cを計算したいのであれば：

>>> a = np.array([2,3,4,5])
>>> b = np.array([8,5,4])
>>> c = np.array([5,4,6,8,3])
>>> ax,bx,cx = np.ix_(a,b,c)
>>> ax
array([2,
       3,
       4,
       5])
>>> bx
array([[[8],
        [5],
        [4]]])
>>> cx
array([5, 4, 6, 8, 3])
>>> ax.shape, bx.shape, cx.shape
((4, 1, 1), (1, 3, 1), (1, 1, 5))
>>> result = ax+bx*cx
>>> result
array([[[42, 34, 50, 66, 26],
        [27, 22, 32, 42, 17],
        [22, 18, 26, 34, 14]],
       [[43, 35, 51, 67, 27],
        [28, 23, 33, 43, 18],
        [23, 19, 27, 35, 15]],
       [[44, 36, 52, 68, 28],
        [29, 24, 34, 44, 19],
        [24, 20, 28, 36, 16]],
       [[45, 37, 53, 69, 29],
        [30, 25, 35, 45, 20],
        [25, 21, 29, 37, 17]]])
>>> result[3,2,4]
17
>>> a[3]+b[2]*c[4]
17

以下のようにreduceを実装することもできます：

>>> def ufunc_reduce(ufct, *vectors):
...    vs = np.ix_(*vectors)
...    r = ufct.identity
...    for v in vs:
...        r = ufct(r,v)
...    return r

そして、このように使用します：

>>> ufunc_reduce(np.add,a,b,c)
array([[[15, 14, 16, 18, 13],
        [12, 11, 13, 15, 10],
        [11, 10, 12, 14,  9]],
       [[16, 15, 17, 19, 14],
        [13, 12, 14, 16, 11],
        [12, 11, 13, 15, 10]],
       [[17, 16, 18, 20, 15],
        [14, 13, 15, 17, 12],
        [13, 12, 14, 16, 11]],
       [[18, 17, 19, 21, 16],
        [15, 14, 16, 18, 13],
        [14, 13, 15, 17, 12]]])

 

標準のufunc.reduceと比べたこのバージョンのreduceの利点は、出力ｘベクトル数の大きさの引数配列の作成を避けるために、ブロードキャストルールを使用するところにあります。

文字列によるインデックス付け

Recordarraysを参照してください。(参照先不明)

線形代数

執筆中です。基本的な線形代数がここに入ります。

簡単な配列演算

詳細はnumpyフォルダにあるlinalg.pyを参照してください。

>>> import numpy as np
>>> a = np.array([[1.0, 2.0], [3.0, 4.0]])
>>> print(a)
[[ 1.  2.]
 [ 3.  4.]]

>>> a.transpose()
array([[ 1.,  3.],
       [ 2.,  4.]])

>>> np.linalg.inv(a)
array([[-2. ,  1. ],
       [ 1.5, -0.5]])

>>> u = np.eye(2) # unit 2x2 matrix; "eye" represents "I"
>>> u
array([[ 1.,  0.],
       [ 0.,  1.]])
>>> j = np.array([[0.0, -1.0], [1.0, 0.0]])

>>> np.dot (j, j) # matrix product
array([[-1.,  0.],
       [ 0., -1.]])

>>> np.trace(u)  # trace
2.0

>>> y = np.array([[5.], [7.]])
>>> np.linalg.solve(a, y)
array([[-3.],
       [ 4.]])

>>> np.linalg.eig(j)
(array([ 0.+1.j,  0.-1.j]), array([[ 0.70710678+0.j        ,  0.70710678-0.j        ],
       [ 0.00000000-0.70710678j,  0.00000000+0.70710678j]]))
Parameters:
    square matrix
Returns
    The eigenvalues, each repeated according to its multiplicity.
    The normalized (unit "length") eigenvectors, such that the
    column ``v[:,i]`` is the eigenvector corresponding to the
    eigenvalue ``w[i]`` .

ヒントとコツ

ここでは、ちょっとした役立つTipsを提供します。

「自動的な」再整形

配列の次元を変更する場合、配列のサイズを省略し、自動的に推定させることができます。

>>> a = np.arange(30)
>>> a.shape = 2,-1,3  # -1 means "whatever is needed"
>>> a.shape
(2, 5, 3)
>>> a
array([[[ 0,  1,  2],
        [ 3,  4,  5],
        [ 6,  7,  8],
        [ 9, 10, 11],
        [12, 13, 14]],
       [[15, 16, 17],
        [18, 19, 20],
        [21, 22, 23],
        [24, 25, 26],
        [27, 28, 29]]])

ベクトルの積み上げ

同じサイズを持つ行ベクトルのリストから、どのように2次元配列を作成するのでしょうか。MATLABでは、これは非常に簡単です：「ｘ」と「ｙ」が同じ長さを持つ2つのベクトルの場合、「m=[x;y]」とするだけです。NumPyでは、 積み上げを実行する次元に従って「column_stack」や「dstack」、「hstack」、「vstack」といった関数で実施します。例えば：

x = np.arange(0,10,2)                     # x=([0,2,4,6,8])
y = np.arange(5)                          # y=([0,1,2,3,4])
m = np.vstack([x,y])                      # m=([[0,2,4,6,8],
                                          #     [0,1,2,3,4]])
xy = np.hstack([x,y])                     # xy =([0,2,4,6,8,0,1,2,3,4])

2次元以上でのこれらの関数のロジックは、奇妙ではあります。

関連項目

Numpy for Matlab users

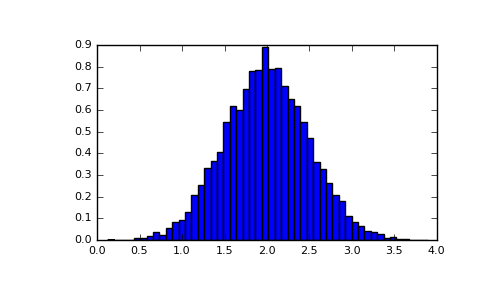
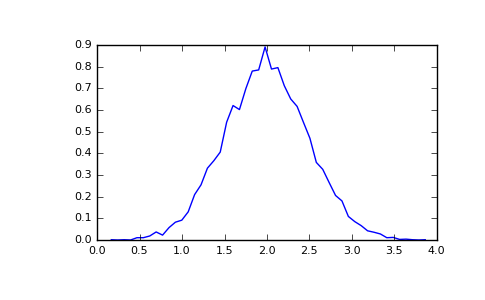
ヒストグラム

配列に適用されるNumPyの「histgram」関数は、ベクトルのペア、つまり配列のヒストグラムとビンのベクトルを返します。

注意：matplotlibにもヒストグラムを生成する関数 (Matlabでは「hist」と呼ばれます) がありますが、NumPyとは異なります。主な違いは、「pylab.hist」は自動的にヒストグラムを描画し、「numpy.histgram」はデータを生成するのみであることです。

>>> import numpy as np
>>> import matplotlib.pyplot as plt
>>> # Build a vector of 10000 normal deviates with variance 0.5^2 and mean 2
>>> mu, sigma = 2, 0.5
>>> v = np.random.normal(mu,sigma,10000)
>>> # Plot a normalized histogram with 50 bins
>>> plt.hist(v, bins=50, normed=1)       # matplotlib version (plot)
>>> plt.show()

f:id:masakykato:20170202201220p:plain

>>> # Compute the histogram with numpy and then plot it
>>> (n, bins) = np.histogram(v, bins=50, normed=True)  # NumPy version (no plot)
>>> plt.plot(.5*(bins[1:]+bins[:-1]), n)
>>> plt.show()

f:id:masakykato:20170202201251p:plain

参考情報

 

データサイエンスにおけるETL vs ELT

データサイエンス全般

ETLといえば、昔からBIの領域で様々なマスター／トランザクションデータを収集するために使われている技術です。すなわち、Extract (抽出) － Transform (変換) － Load (読み込み) という3つのプロセスで、BI側に役立つ形にデータを加工して取り込むことです。

 

これに対してELTという技術もあります。これはTransformとLoadの順番が逆のプロセスになっているもので、ETLアーキテクチャでは中間層がボトルネックになりやすいという問題を解消させる考え方です。例えばOracle社のData Integratorは、ELTアーキテクチャを採用してデータ変換をOracle Databaseのエンジン内で行うことにより、中間層がボトルネックになることを避けています。

 

このようにETLとELTという言葉はアーキテクチャの視点でのみ使われていると思っていたのですが、以下のブログから、データサイエンスの領域では異なった視点からELTという言葉が使われていることに気が付きました。

https://buckwoody.wordpress.com/2016/11/18/data-wrangling-elt-not-etl/

データサイエンスの目的は、BIのようにデータを可視化することではなくデータから答えを見つけ出すことにあるため、オリジナルのデータが非常に重要になります。このため、データ変換は最後にすべきことからETLプロセスではなくELTプロセスであるべきだということです。

 

機械学習のみでなく統計処理でもデータ処理のプロセスは確かにELTだったのですが、この言葉が使われているということには、うかつにも気が付きませんでした。

従来の統計処理と機械学習

AI 機械学習 深層学習

最近様々な新聞や雑誌に、毎日のように機械学習(マシンラーニング)や深層学習(ディープラーニング)といった言葉がでてきますが、先日あるお客様より

「今までの統計処理と何が違うの？人工知能とはどう違うの？」

という質問をされました。

 

機械学習の使用してる数学的な手法やアルゴリズムは従来の統計処理(統計解析やデータマイニング)と非常に近いため、何が違うのかがよく分からないという人が多いような気がするので、このブログの最初のネタにしようと思います。

 

なおここで書いている内容は、あくまで解釈の一つとして理解ください。視点によっては違う解釈のほうが適合しやすいことがあります。

 

まず、

機械学習、深層学習 ＝ 人工知能

ではないですよね。機械学習や深層学習は、人工知能のための技術、もしくは研究テーマの一つであるという考え方です。

 

機械学習と深層学習についてですが、別々のもののように扱われている記事をよく見かけますが、深層学習は多層ニューラルネットワークを用いた機械学習の手法の一つです。ただし、深層学習は従来の機械学習の手法では難しかった画像、音声、言語を対象とする人工知能のテーマに対して優れた性能を発揮するため、独自のテーマとして脚光を浴びているという背景があるのだと思います。

 

ここまでで、先ほどのお客様からの質問に対して

「人工知能 ← (適用技術/研究テーマ) － 機械学習(深層学習含む)」

という回答になりました。

 

次に従来の統計処理との違いについてですが、先ほども書いたように機械学習と従来の統計処理の数学的な手法やアルゴリズムは非常に近いのですが、目的が異なります。つまり

  • 統計解析は、まず仮説を立て、その仮説を標本データから推定、評価していくことで、仮説の正しさを検証するものです。つまり、データの意味や仮説を説明することに重きを置いています。
  • データマイニングは、膨大なデータからルールやパターンを発見し、検証するものです。つまり事実の発見と説明に重きを置いています。
  • 機械学習は、膨大なデータからルールやパターンを発見し、それを基に予測することを目的とするものです。つまり事実から予測をすることに重きを置いています。

 

なお、一般的に「予測」というと「未来を予測する」ことと思われますが、機械学習分野においては、「未来を予測する」ことだけではなく「見えないものを見えるようにする」ことにも予測という言葉を使います。例えばある企業が提供しているサービスを利用している顧客に対して、「3か月後にサービス利用を停止する顧客を予測する」ことも予測ですし、「今サービス利用を停止しようと考えている顧客を探し出す」ことも予測と言えます。

 

以上で、先ほどのお客様からの質問に対して、

「従来の統計処理との違いは目的」

という回答になりますね。

 

なお、別の解釈がある、こういう回答のほうがお客様が分かりやすい、という話がありましたら、是非ともコメント頂ければと思います。